如何利用線性迴歸(Linear Regression)分析計算阻尼係數(Damping Ratio)

Photo by Kelly Sikkema on Unsplash
什麼是阻尼係數?有什麼用?
什麼是阻尼?阻尼是振動領域很常使用的一個性質,主要特性是能抵銷能量,且抵銷能量的能力會隨著速度越快而越強大。 以下引述維基百科:
阻尼(英語:damping)是指任何振動系統在振動中,由於外界作用(如流體阻力、摩擦力等)和/或系統本身固有的原因引起的振動幅度逐漸下降的特性,以及此一特性的量化表徵。
一個有阻尼的彈簧振子振動示意圖。從振動形式看,這是一個次阻尼體系。 在實際振動中,由於摩擦力總是存在的,所以振動系統最初所獲得的能量,在振動過程中因阻力不斷對系統做負功,使得系統的能量不斷減少,振動的強度逐漸減弱,振幅也就越來越小,以至於最後的停止振動,像這樣的因系統的力學能,由於摩擦及轉化成內能逐漸減少,振幅隨時間而減弱振動,稱為阻尼振動。
所以阻尼特性就是決定物體受外力擾動後,振動多久才會停止的特性。 為了定義阻尼的大小,所以有了阻尼係數來評估。 但不是阻尼越大越好,有些門的設計是會慢慢自動關上,用力去關反而會產生很大的阻力還不會快多少,這就是過阻尼的狀況。
計算阻尼係數的兩種方式:絕對與相對
所以能知道一個物體 (系統)的阻尼係數對判斷反應時間的特性上就非常重要。實務上我們可以讓物體自由震盪,並量測反應過程的特性如位移,加速度對上時間的曲線。 通常單自由度的系統會產生如下圖的隨時間而衰減的曲線,阻尼係數則是決定衰減速度快慢的因素之一(另外一個因素是自然振動頻率)。
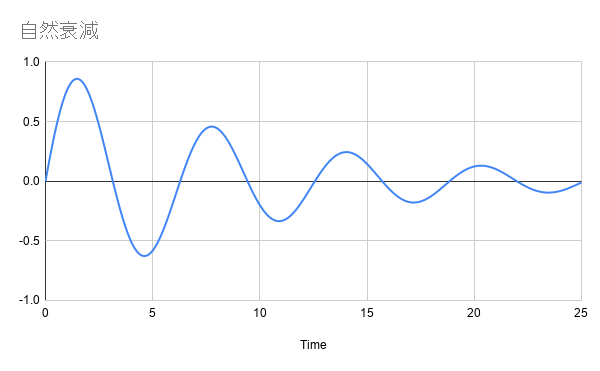
利用傅立葉轉換成頻譜就可以得到自然振動頻率。只要找出需要多少時間收斂,就可以進而計算該物體的阻尼係數。
而如何找出收斂時間呢? 基本上有兩種做法,分別是絕對與相對。
絕對
絕對的評估方式是,當震盪的 peak 值小於某個數值以下,就視為已收斂。
PS. 將 Raw data 進行傅立葉轉換與找出 local peak 可以使用程式語言進行運算。我個人是利用 Python 內的 SciPy package.
但是絕對的方式有幾個問題,第一個是到底收斂到多小的數值才算收斂?第二個問題是當振幅越大時,所得到的收斂時間就會大於振幅小的情況,就算兩者的阻尼係數與頻率均相同。如下圖:
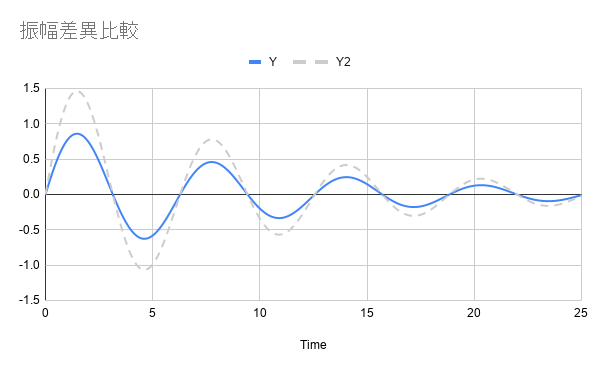
兩者的阻尼係數與頻率均相同,但是使用絕對的方式評估下會得到不同的收斂時間
相對
相對的意思則是當震盪的 peak 值小於最大值的一定比例(比如收斂到小於 2%),視為已收斂。 相較之下,相對的方式就會比較合理,可以排除振幅不同造成的影響。
利用線性迴歸分析計算阻尼係數
而是否只能藉由找出時間才能計算阻尼係數呢? 其實有另外更適合的方式,那就是採用線性迴歸來計算。 藉由剛剛的例子,本身收斂的包絡線會依照以下公式衰減。
$$ y=Ae^{-2 \pi \zeta f t} $$
其中 $$\zeta$$ 是阻尼係數, $$\pi$$ 是圓周率, $$f$$是自然振動頻率
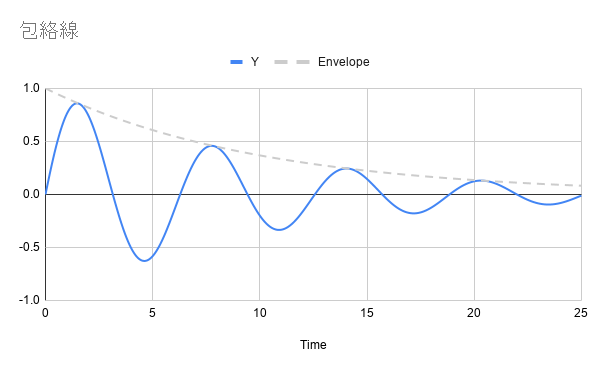
灰色虛線為包絡線
所以當 $$f$$ 已知(藉由傅立葉轉換)的狀況下,求出 $$\zeta$$ 就會相對簡單。
而求出阻尼係數是如何與線性迴歸有關係呢?其實只要簡單的做一下轉換 (公式兩邊取對數) 就可以把原本指數衰減 (Exponential decay) 轉換成線性公式
$$ \ln y=\ln A -2 \pi \zeta f t \implies Y = \beta_0 + \beta_1 t $$
其中 $$-2 \pi \zeta f$$ 就是 $$\beta_1$$ ,也就是直線的斜率。
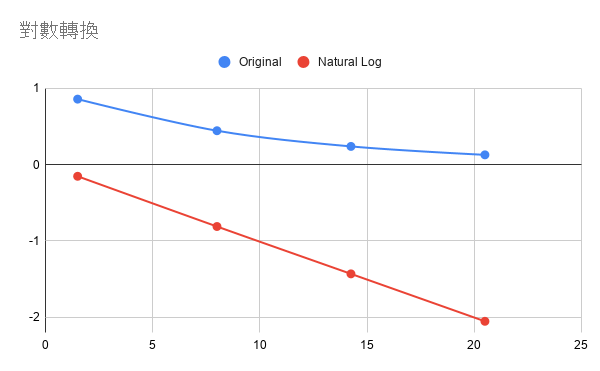
藍色為原本的包絡線,紅色為對數轉換後的包絡線。可以明顯看出轉換後唯一直線。
利用程式 (如 Python, R 甚至是 Excel) 即可計算出 $$\beta_1$$ 的最佳估計值。參考公式
總結一下利用自然震動的衰減資料找出阻尼係數的步驟:
- 利用傅立葉轉換計算出自然振動頻率 (Python Scipy package)
- 找出 local peak 值與相對應的時間點位 (Python Scipy package)
- 對 local peak 的 Y 軸資料取自然對數 (natural log),轉換成直線
- 針對轉換後的資料進行迴歸分析,求得斜率 $$\beta_1$$ ,將 $$\beta_1$$ 除以自然振動頻率即可得到阻尼係數 $$\zeta$$ 。
如此一來,我們就可以計算出上述例子的阻尼係數為。該例估計的 $$\beta_1$$ 為 -0.1,而自然頻率為 0.16Hz,所以得到阻尼係數為 0.0995。
PS. 本篇主要介紹如何利用迴歸分析計算阻尼係數的概念,計算自然頻率、找出 local peak 以及迴歸分析的程式碼會其他相關文章再詳細介紹。
使用迴歸分析的好處?
用回歸分析來找阻尼係數看起來需要用到對數轉換與統計分析,似乎比起用相對的方式找出時間要麻煩許多,但是這個方式在實務使用上有許多優勢:
- 量測資料非理想資料,會有環境、設備等誤差影響造成誤判。使用迴歸分析可以將所有點納入考量,不受特定點偏差的影響。
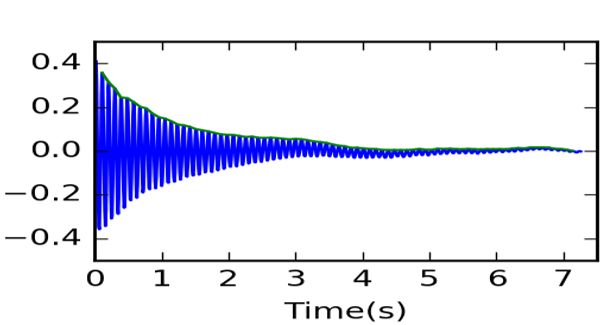
這張圖是實務上量測出來的數據,可以看出約 3 秒後的數據受到雜訊擾動
- 轉換成直線而非曲線,適合肉眼直接觀察,檢測出差異,並且例用迴歸分析的 $$R^2$$ 的數值來量化收斂狀況是否穩定。如下列圖組表示:
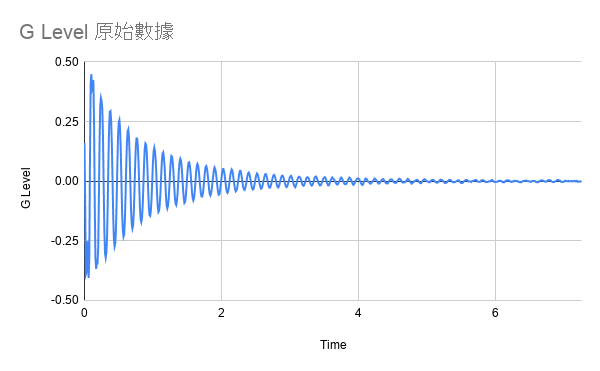
這張圖為實務上原始數據
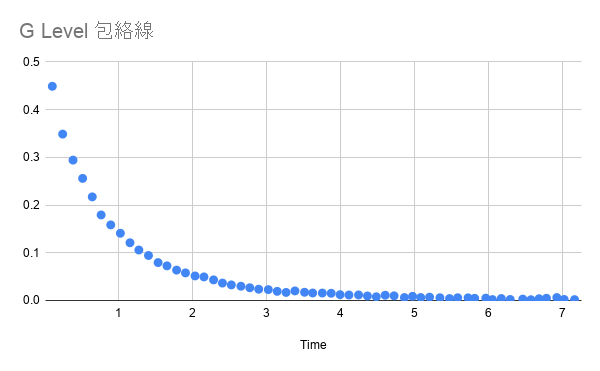
此圖為包絡線的原始數據,要看出其收斂的穩定性有相對難度。
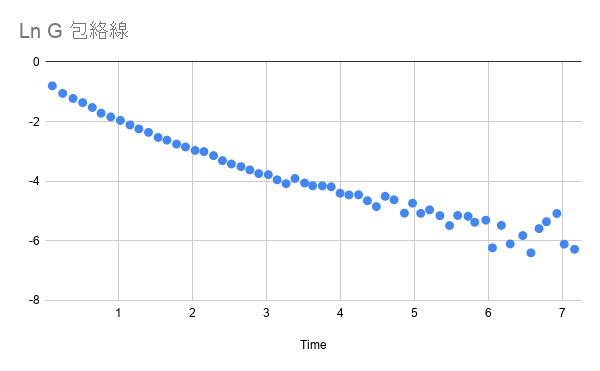
可以看出前段 (3 秒前, $$LnG > -4$$ 前)收斂相對穩定 (接近直線)。3 秒後的數值比較雜亂,應該是數值較低,受到雜訊的影響程度較高。
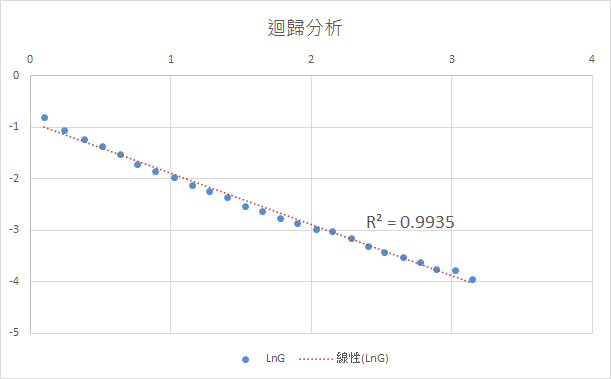
若排除 $$LnG < -4$$ 的數據後進行迴歸分析,得到 $$R^2 = 0.9935$$,表示收斂性非常穩定。
- 只需要足夠的資料進行迴歸分析,不需要一定等到收斂完成才能進行判讀。傳統方法上,如果設定的閥值 (Threshhold) 太小,在記錄資料的時間不足下,抓不到收斂時間,也就無法依此計算阻尼係數。但使用迴歸分析的方式,只要有足夠的 local peaks (大約 15~20 點) ,即可計算出阻尼係數。
線性迴歸分析雖然是很基礎的統計分析工具,但是卻非常萬用,很多生活/工作上的不同場景都有機會套用。像本文介紹的,使用統計分析的眼睛去看數據,可以得到完全不同的分析方式,得到更穩定,更合理的分析結果。
2023/05/14 新增:
利用 Streamlit 建立一個簡易使用的 web app。
有使用上的問題或建議的話,歡迎留言或 email 給我。