Photo by Lucas Lenzi on Unsplash

什麼是彈性模數?

以下引述維基百科

楊氏模數，也稱楊氏模數（英語：Young’s modulus），一般將楊氏模數習慣稱爲彈性模量，是材料力學中的名詞。彈性材料承受正向應力時會產生正向應變，在形變量沒有超過對應材料的一定彈性限度時，定義正向應力與正向應變的比值為這種材料的楊氏模數。公式記為

$$E={\frac {\sigma }{\varepsilon }}$$

其中，$E$ 表示楊氏模數，$\sigma$ 表示正向應力，$\varepsilon$ 表示正向應變。

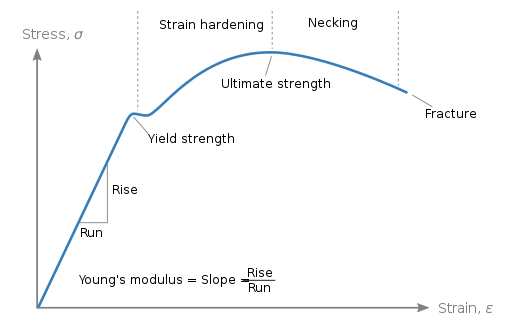
Nicoguaro, CC BY 4.0 https://creativecommons.org/licenses/by/4.0, via Wikimedia Commons

為什麼需要使用迴歸分析?

楊氏模數是評估材料強度的重要參數之一，所以需要盡可能得到準確的楊氏模數。雖然楊氏模數只是線性段的斜率，理論上的計算非常簡單，只要把線性段的任何一點應力除以應變就可以得到。但為什麼還要大費周章使用迴歸分析來計算呢? 我認為問題點如下:

• 線性段區域的範圍不是固定: 有的材料 50MPa 以上就超出線性範圍，但是有的材料則是 300MPa 以上才是。想要自動化的廣泛應用的話就不能取特定應力下的應變值來計算。
• 現實數據並非完美直線: 真正的實驗數據並不會像理論上那樣完美從原點出發，所以必須取線性範圍內的最大與最小應力的兩個點位去計算斜率。且並非線性範圍都維持固定斜率，所以需要肉眼找出線性範圍的位置，當測試數量一多的時候光分析數據就會很花時間。
• 判定直線範圍的方法沒有統一條件: 如果是用肉眼找出線性範圍，則每個人的選完的範圍就會有差異，甚至是每個人在不同時段下選擇的範圍也會有差異。如此就會造成楊氏模數判斷上的差異。

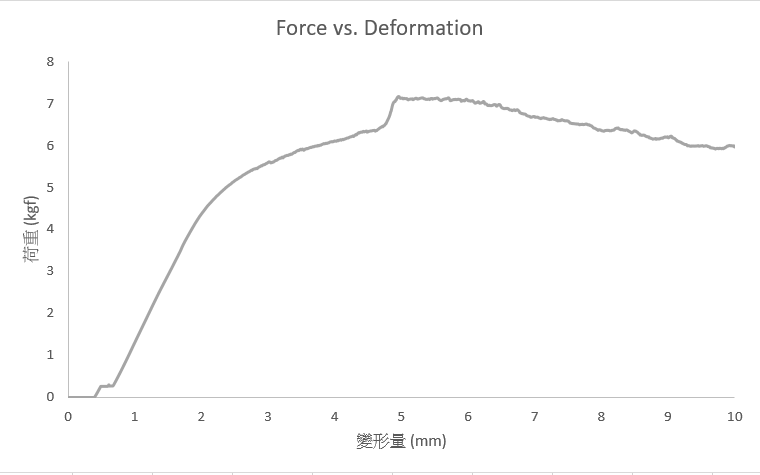
判定直線範圍的方法沒有統一標準

如何使用迴歸分析計算斜率?

如果要使用迴歸分析計算斜率，第一步是要取出直線段。如果要用程式自動化切出直線部分的話，就需要先定義好取出條件。 目前我會建議以下兩種條件:

1. 找出應力的最大值，往前取出所有線段。
2. 找出應力的最大值，取出前段應力值介於最大值 20 ~ 80% (上下限可依需求調整，不一定需要固定在 20 跟 80) 之間的線段。

第二步就是取出直線段後，再進行迴歸分析，即可得到斜率，也就是彈性模數。

兩種取直線的方式各有優缺點。第一種方式很泛用，但一開始就會納入很大部分的非直線線段(不論是塑性段還是雜訊)，導致迴歸出來的效果不佳。第二種方式有很大機會排除掉非線性段，讓迴歸出來的斜率準確度高。但是因為每種材料的特性不一，需要針對不同材料微調上下限，比較不泛用。

如何滿足泛用且自動化

所以如果想要自動化且泛用的話，就必須使用第一種方式，但需要加上第三步 - 持續修正。 利用第一種方式做完迴歸後，因為包含比較多的非線性線段，所以得到的直線在後半段接近降伏的部分誤差會較大，也可以明顯看出 $R^2$ 值較差。 下一步便是找出誤差大的部分並加以排除，剩下的部分再次進行迴歸分析。 如此重複以上的循環，直到 $R^2$ 大於某個程度，例如 0.96 以上才停止。此時得到的直線便是這筆測試資料的最佳線性段。 而如果是屬於降伏點不明顯的材料（如大部分的金屬），則可以利用此直線方程式，offset 0.2% 作出新的方程式，將新的方程式延伸找出與原始曲線相交的位置，此位置對應的應力、應變值便是對評估材料強度也很重要的參數：降伏應力與應變。 而如何找出兩條線段的相交點呢？最簡單的方式就是分別取出最大值與非線性段間的數值。通常來說，原始資料在降伏應變前會大於直線方程式計算出來的應力值，降伏應變後則會小於。所以只要將兩者相減，找出變號的位置，即是降伏點。

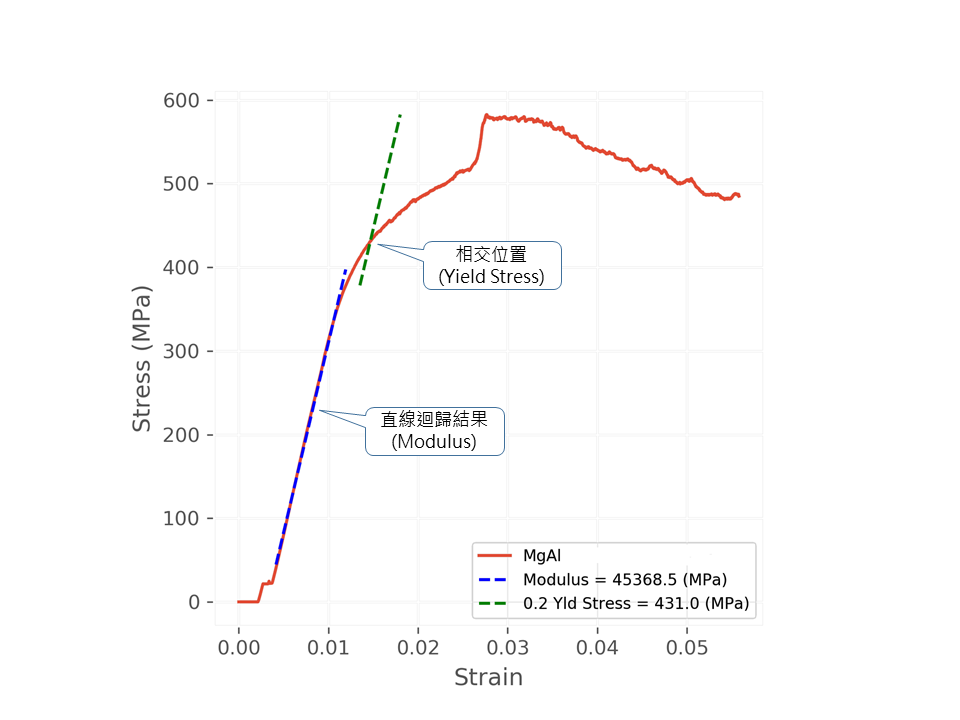
利用迴歸分析找出直線區域與計算降伏應力

結論

利用迴歸分析找出斜率的方式可以應用在很多不同的領域與狀況。用這種方法搭配簡易的程式語言，就可以準確而且大量自動化分析數據。 利用程式語言搭配迴歸分析解析數據是我這幾年以來最常用的數據分析手法。學習基本的程式開發與統計分析，則是我這幾年來最划算的時間投資。

2023/05/20 新增:

利用 Streamlit 建立一個簡易使用的 web app。

有使用上的問題或建議的話，歡迎留言或 email 給我。

Demo App by Streamlit